Contoh Soal Cerita Determinan dan Invers Matriks

Contoh Soal Cerita Determinan dan Invers Matriks

Nama: Dasya Putrinda Haris (08) 

Kelas: XI IPS 2

Contoh 5: Perusahaan Ban Mobil dan Truk

JTire merupakan suatu perusahaan ban yang menjual dua jenis ban, ban mobil dan truk, kepada tiga distributornya. Distributor yang ada di Jakarta selama bulan Januari, Februari, dan Maret berhasil menjual ban mobil sebanyak 350, 420, dan 530 serta ban truk sebanyak 220, 180, dan 140. Sementara itu, distributor yang ada di Tangerang berhasil menjual ban mobil sebanyak 430, 560, dan 690 serta ban truk sebanyak 280, 320, dan 220 pada 3 bulan yang sama. Sedangkan distributor yang ada di Bekasi berhasil menjual ban mobil sebanyak 864, 980, dan 1.236 serta ban truk sebanyak 535, 542, dan 332 pada periode yang sama.

1. Tulislah “matriks penjualan” berordo 2 × 3 untuk setiap distributor (J untuk Jakarta, T untuk Tangerang, dan B untuk Bekasi), dengan kolom-kolom Januari, Februari, dan Maret, serta dua baris yang menunjukkan jenis ban mobil dan ban truk.
2. Dengan menggunakan matriks pada poin 1, tentukan selisih banyaknya ban yang dijual oleh distributor di Bekasi untuk setiap jenisnya dengan jumlah ban yang dijual oleh distributor yang berada di Jakarta dan Tangerang.
3. Tren pasar menunjukkan bahwa untuk tiga bulan dalam tahun berikutnya, penjualan ban yang dilakukan oleh distributor di Jakarta mengalami kenaikan 10%, sedangkan penjualan yang dilakukan oleh distributor di Tangerang mengalami penurunan 3%, dan distributor di Bekasi tidak mengalami peningkatan atau penurunan dalam penjualannya. Berapa jumlah total banyaknya ban yang akan bisa dijual oleh semua distributor JTire tahun depan, untuk setiap jenisnya?

Pembahasan

1. Pertama, kita buat tabel penjualan yang terdiri dari kolom-kolom bulan (Januari, Februari, dan Maret) dan baris-baris yang menyatakan jenis ban. Berikut ini tabel penjualan dari distributor di Jakarta.
   
   Sedangkan tabel penjualan distributor Tangerang adalah sebagai berikut.
   
   Berikut ini tabel penjualan distributor Bekasi.
   
   Sehingga kita mendapatkan matriks J, T, dan B sebagai berikut.
   
2. Selisih banyaknya ban yang dijual oleh distributor di Bekasi untuk setiap jenisnya dengan jumlah ban yang dijual oleh distributor yang berada di Jakarta dan Tangerang dapat ditentukan sebagai berikut.
   
   Sehingga, dari matriks di atas kita peroleh bahwa banyaknya ban mobil yang dijual oleh distributor di Bekasi pada bulan Januari dan Maret secara berturut-turut 84 dan 16 lebih besar dari jumlah penjualan distributor Jakarta dan Tangerang. Sedangkan pada bulan Februari banyaknya penjualan ban mobil di distributor Bekasi sama dengan yang di Jakarta dan Tangerang. Penjualan ban truk yang dilakukan distributor Bekasi lebih banyak 35 dan 42 dibandingkan distributor di Jakarta dan Tangerang. Sedangkan penjualan ban truk distributor di Bekasi 28 kurangnya dari distributor Jakarta dan Tangerang.
3. Jumlah total banyaknya ban yang akan bisa dijual oleh semua distributor JTire tahun depan, untuk setiap jenisnya dapat ditentukan dengan mengoperasikan perkalian skalar serta penjumlahan dan pengurangan pada matriks-matriks J, T, dan B.Penjualan ban yang dilakukan oleh distributor di Jakarta mengalami kenaikan 10%, artinya tahun depan banyaknya ban yang dijual adalah 100% + 10% = 110% = 1,1 dari banyaknya ban yang dijual tahun ini. Karena tren penjualan distributor di Tangerang mengalami penurunan 3%, maka banyaknya ban yang dijual tahun depan 100% – 3% = 97% = 0,97 dari banyaknya ban yang terjual tahun ini.
   
   Sehingga banykanya ban mobil yang dijual oleh JTire pada bulan Januari, Februari, dan Maret secara berturut-turut kurang lebih 1.666, 1.985, dan 2.488. Sedangkan banyaknya ban truk yang dijual pada ketiga bulan tersebut adalah 1.049, 1.050, dan 699.

Contoh 6: Bergabung dengan Kelompok Belajar

Di setiap awal tahun pembelajaran, siswa-siswa di suatu SMA yang berminat di dalam kelompok belajar tertentu melakukan pendaftaran. Banyaknya siswa laki-laki dan perempuan yang medaftar dapat dikelompokkan berdasarkan kelasnya. Informasi ini disajikan dalam matriks J. Banyaknya siswa laki-laki dan perempuan dari masing-masing kelas yang diproyeksikan untuk bergabung ke dalam kelompok belajar disajikan dalam matriks C. Hitunglah perkalian matriks JC dan gunakan hasilnya untuk menjawab pertanyaan-pertanyaan berikut.

1. Perkirakanlah berapa banyak siswa perempuan yang bergabung dengan kelompok belajar matematika.
2. Berapakah kemungkinan banyaknya siswa laki-laki yang bergabung dengan kelompok belajar Fisika?
3. Apakah representasi dari elemen P13 dari matriks hasil?

Pembahasan Perkalian matriks JC dapat dilakukan sebagai berikut.

1. Banyaknya siswa perempuan yang akan bergabung dengan kelompok belajar matematika direpresentasikan dengan P₁₁, yaitu 32 (pembulatan).
2. Kemungkinan banyaknya siswa laki-laki yang bergabung dengan kelompok belajar Fisika direpresentasikan oleh elemen P₂₂, yaitu 10.
3. Elemen P₁₃ merupakan hasil penjumlahan dari perkalian elemen-elemen yang bersesuaian di baris pertama matriks J (perempuan) dan kolom ketiga dari matriks C (kimia), sehingga elemen P₁₃, yaitu 21,3 (dibulatkan menjadi 21), merepresentasikan kemungkinan banyaknya siswa perempuan yang akan bergabung dengan kelompok belajar kimia.

Contoh 7:

Arman membeli 5 pensil dan 3 penghapus, sedangkan Susi membeli 4 pensil dan 2 penghapus di toko yang sama. Di kasir, Arman membayar Rp 11.500,00 sedangkan Susi membayar Rp 9.000,00. Jika Dodi membeli 6 pensil dan 5 penghapus, berapa ia harus membayar?

Persoalan ini dapat diselesaikan menggunakan dua cara.

Jika  maka dengan cara pertama, yakni cara invers, diperoleh .

Ingat, determinan dari  adalah ad - bc.

Penyelesaian cara kedua adalah cara determinan, yaitu:

Penyelesaian

Dimisalkan harga satuan pensil = x dan harga satuan penghapus = y. Disusun ke dalam sistim persamaan linear dua variabel (SPLDV)

5x + 3y = 11.500

4x + 2y = 9.000

Sistim persamaan di atas dapat dinyatakan dalam bentuk matriks, yakni

Cara Pertama (Invers Matriks)

  

  

  

 dan 

Diperoleh harga satuan pensil Rp 2.000 dan harga satuan penghapus Rp 500.

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500

-------------------------

Cara Kedua (Determinan Matriks)

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500.

Contoh 8 Perusahaan Pakaian:

Suatu perusahaan pakaian, JCloth, memiliki dua pabrik yang terletak di Surabaya dan Malang. Di dua pabrik tersebut, JCloth memproduksi dua jenis pakaian, yaitu kaos dan jaket. Perusahaan tersebut memproduksi pakaian yang kualitasnya dapat dibedakan menjadi tiga jenis, yaitu standard, deluxe, dan premium. Tahun kemarin, pabrik di Surabaya dapat memproduksi kaos sebanyak 3.820 kualitas standard, 2.460 kualitas deluxe, dan 1.540 kualitas premium, serta jaket sebanyak 1.960 kualitas standard, 1.240 kualitas deluxe, dan 920 kualitas premium. Sedangkan pabrik yang terletak di Malang dapat memproduksi kaos sebanyak 4.220 kualitas standard, 2.960 kualitas deluxe, dan 1.640 kualitas premium, serta jaket sebanyak 2.960 kualitas standard, 3.240 kualitas deluxe, dan 820 kualitas premium dalam periode yang sama.

1. Tulislah “matriks produksi” dengan ordo 3 × 2 untuk masing-masing pabrik (S untuk Surabaya dan M untuk Malang), dengan kolom kaos, kolom jaket, dan tiga baris yang menunjukkan banyaknya jenis-jenis pakaian yang diproduksi.

2. Gunakan matriks dari poin 1 untuk menentukan banyaknya pakaian yang telah diproduksi oleh pabrik di Surabaya dan Malang.

3. Gunakan perkalian skalar untuk menentukan berapa banyak pakaian dari masing-masing jenis yang akan diproduksi di Surabaya dan Malang, jika perkiraan peningkatan produksinya adalah 4%.

4. Berapa total banyak pakaian yang diproduksi oleh JCloth (di kedua pabrik) pada tahun depan, untuk setiap jenis pakaian?

Pembahasan

1. Agar lebih mudah dalam membuat matriks produksi, pertama kita akan membuat tabel produksi untuk masing-masing pabrik sebagai berikut.
   
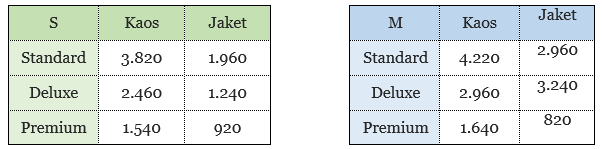
   Sehingga, kita mendapatkan matriks-matriks produksi S dan M sebagai berikut.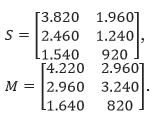
   
2. Dari matriks yang diperoleh dari poin 1, kita dapat menghitung banyaknya pakaian yang telah diproduksi oleh pabrik di Surabaya. Banyaknya kaos yang telah diproduksi adalah 7.820, sedangkan banyaknya jaket yang sudah diproduksi adalah 4.120. Selanjutnya, banyaknya kaos yang diproduksi oleh pabrik di Malang adalah 8.820, sedangkan banyaknya jaket yang telah diproduksi adalah 7.020.
3. Diketahui perkiraan peningkatan produksinya adalah 4% = 0,04. Artinya, jika n adalah banyaknya produksi pakaian tahun kemarin, maka banyaknya produksi pada tahun ini adalah n + 0,04n = 1,04n. Sehingga, matriks produksi pada tahun depan dapat ditentukan dengan menggunakan perkalian skalar sebagai berikut.

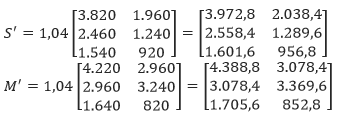
Sehingga dari matriks di atas kita mendapatkan perkiraan banyaknya pakaian yang akan diproduksi oleh JCloth di pabrik Surabaya ataupun Malang. Pabrik di Surabaya akan memproduksi kaos kurang lebih 3.973 kualitas standard, 2.558 kualitas deluxe, dan 1.602 kualitas premium serta memproduksi jaket sebanyak 2.038 kualitas standard, 1.290 kualitas deluxe, dan 956,8 kualitas premium. Sedangkan pada, pabrik di Malang akan memproduksi kaos sebanyak 4.389 kualitas standard, 3.078 kualitas deluxe, 1.706 kualitas premium serta meproduksi jaket sebanyak 3.078 kualitas standard, 3.370 kualitas deluxe, dan  852,8 kualitas premium pada periode yang sama.

Untuk menentukan banyaknya total pakaian yang diproduksi oleh JCloth, kita jumlahkan matriks S’ dengan M’ seperti berikut.

Dari penjumlahan matriks di atas, kita memperoleh informasi banyaknya pakaian yang akan diproduksi oleh JCloth. Dengan menjumlahkan semua elemen-elemen matriks penjumlahan tersebut, kita peroleh bahwa banyaknya pakaian yang akan diproduksi oleh JCloth kurang lebih 28.142.

Contoh 9: Musik Klasik

Klasik FM melakukan acara amal yang dapat diikuti oleh pendengar setianya ataupun umum. Sebagai pendengar setia radio tersebut, Rangga memutuskan akan menyumbangkan sejumlah uang berdasarkan komposer musik favoritnya untuk tiga hari ke depan. Setiap kali musik favoritnya mengudara, dia akan menyumbangkan: Rp 30.000,- untuk setiap lagunya Mozart, Rp 25.000,- untuk setiap lagunya Beethoven, dan Rp 20.000,- untuk setiap lagunya Vivaldi. Informasi ini disajikan oleh Tabel 3.1. Banyaknya lagu yang dia dengar dari masing-masing komposer disajikan pada Tabel 3.2. Hitunglah hasil kali DC dan interpretasikan apa yang direpresentasikan oleh masing-masing elemennya.

Pembahasan Tabel 3.1 dan Tabel 3.2 di atas dapat dijadikan menjadi matriks-matriks C dan D sebagai berikut.

Sehingga, matriks perkalian DC dapat ditentukan sebagai berikut.

Elemen-elemen matriks DC tersebut merepresentasikan jumlah uang Rangga yang disumbangkan ke Klasik FM pada hari Senin, Selasa, dan Rabu, yang secara berturut-turut adalah Rp 235.000,00, Rp 200.000,00, dan Rp 310.000,00.

Contoh 10: Perusahaan Meja Biliar

YBiliar, suatu perusahaan pembuat meja biliar, membuat tiga jenis meja biliar, untuk rumahan, penggunaan komersial, dan penggunaan profesional. Banyaknya waktu yang dibutuhkan untuk merakit, mengangkut, dan memasang meja biliar tersebut terangkum dalam matriks T, dimana semua waktunya dalam jam. Biaya masing-masing komponen tersebut dalam rupiah tiap jamnya tersaji dalam matriks C untuk kedua gudang perusahaan tersebut, yaitu Lumajang dan Banyuwangi.

1. Berapakah biaya untuk merakit, mengangkut, dan memasang meja biliar komersial dari gudang yang berada di Lumajang?
2. Berapakah biaya untuk merakit, mengangkut, dan memasang meja biliar komersial dari gudang yang berada di Banyuwangi?
3. Hitunglah perkalian matriks TC dan interpretasikan masing-masing elemennya.

Pembahasan

1. Biaya merakit dari gudang Lumajang dapat ditentukan dengan mengalikan elemen t21 dengan c11, yaitu 1,5 × Rp 100.000,00 = Rp 150.000,00. Sedangkan biaya mengangkutnya dapat diperoleh dengan mengalikan elemen t22 dengan c21, yaitu 0,5 × Rp 120.000,00 = Rp 60.000,00. Biaya memasangnya dapat ditentukan dengan mengalikan elemen t23 dengan c31, yaitu 2,2 × 135.000,00 = Rp 297.000,00.
2. Biaya merakit dari gudang yang berada di Banyuwangi dapat ditentukan dengan mengalikan elemen t21 dengan c12, yaitu 1,5 × Rp 80.000,00 = Rp 120.000,00. Biaya mengangkutnya dapat diperoleh dengan mengalikan elemen t22 dengan c22, yaitu 0,5 × Rp 105.000,00 = Rp 52.500,00. Sedangkan biaya memasangnya dapat ditentukan dengan mengalikan elemen t23 dengan c32, yaitu 2,2 × 125.000,00 = Rp 275.000,00.
3. Perkalian matriks TC dapat ditentukan sebagai berikut.
   
   Baris pertama pada matriks TC menunjukkan jumlah total biaya untuk membuat meja biliar rumahan dari gudang Lumajang dan Banyuwangi. Baris kedua, menunjukkan jumlah total biaya untuk membuat meja biliar komersial dari gudang Lumajang dan Banyuwangi. Sedangkan baris ketiga menunjukkan jumlah total biaya untuk membuat meja biliar profesional dari gudang Lumajang dan Banyuwangi.

Terima kasih kepada berbagai sumber dibawah telah membantu saya mengerjakan tugas yang dibeir, semua soal dibuat oleh para penulis sesuai sumber dibawah dan saya bertugas untuk mengumpulkan berbagai macam sumber dan mempelajarinya.

https://brainly.co.id/tugas/1476814

https://www.ilmusosial.id/2019/12/contoh-soal-cerita-matriks-dalam.html

https://yos3prens.wordpress.com/2014/12/07/5-soal-dan-pembahasan-penerapan-penjumlahan-dan-perkalian-matriks/2/

http://kuncijawaban4.blogspot.com/2017/02/soal-cerita-matriks.html