Luas dan Volume Daerah yang Berkaitan dengan Integral dan Contoh Soal

Luas dan Volume Daerah yang Berkaitan dengan Integral

Nama: Dasya Putrinda H.

Absen: 9

Kelas: 11 IPS 2

Sumber: https://tanya-tanya.com/contoh-soal-dan-pembahasan-bab-integral/

Contoh Soal:

Tentukan luas daerah yang dibatasi oleh 2 grafik yaitu grafik 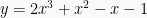$y = 2x^3 + x^2 - x - 1$ dan grafik $y = x^3 + 2x^2 - x - 1$ .

Pembahasan:

Kedua grafik dibuat persamaan f(x) – g(x) untuk mendapat titik potong:

$2x^3 + x^2 - x - 1 = x^3 + 2x^2 + 5x - 1$

$x^3 - x^2 - 6x = 0$

$(x+2)(x)(x-3) = 0$

Akar-akarnya merupakan titik potong kedua grafik yaitu x = -2, x = 0, x = 3.

Maka luas grafik tersebut adalah:

$A =\int^b_a f(x) - g(x) dx$ = $\int^c_a f(x) - g(x) dx + \int^b_c f(x) - g(x) dx$

Dengan a = -2, b = 3, dan c = 0, maka

$A =\int^0_{-2} f(x) - g(x) dx = \int^0_{-2} x^3 - x^2 - 6x dx$ = $[\frac{1}{4}x^4 - \frac{1}{3}x^3 - \frac{6}{2}x^2]^0_{-2}$

$= 0 - (\frac{1}{4}(-2)^4 - \frac{1}{3}(-2)^3 - \frac{6}{2}(-2)^2)$

$= 0 - (\frac{16}{4} - \frac{8}{3} - 12)$ = $- (\frac{48 + 32 - 144}{12}) = \frac{64}{12}$

$A =\int^3_0 f(x) - g(x) dx = \int^3_0 x^3 - x^2 - 6x dx$ = $[\frac{1}{4}x^4 - \frac{1}{3}x^3 - \frac{6}{2}x^2]^3_0$

$= (\frac{1}{4}(3)^4 - \frac{1}{3}(3)^3 - \frac{6}{2}(3)^2) - 0$ = $\frac{81}{4} - 9 - 27 = - \frac{63}{4}$

Nilai $- \frac{63}{4}$ memiliki tanda (-) mengartikan pada interval 0 ≤ x ≤ 3 kurva g(x) > f(x), sehingga penulisan integran terbalik. Seharusnya: g(x) – f(x). Luas tidak mungkin (-) sehingga yang dijumlahkan adalah $\frac{63}{4}$ . Sebagai berikut: