Barisan dan Deret Aritmatika Kelas 11
- Get link
- X
- Other Apps
Barisan dan Deret Aritmatika
Nama/Absen=Dasya Putrinda Haris (09)
Kelas= XI IPS 2
Barisan Aritmatika
Rumusan Barisan Aritmatika
Suku-sukunya dinyatakan dengan rumus berikut :
U1, U2, U3, ….Un
a, a+ b, a+2b, a + 3b, …., a + (n-1) b
Selisih (beda) dinyatakan dengan b
b = U2 – U1 = U3 – U2 = Un – Un – 1
Suku ke n barisan aritmatika (Un) dinyatakan dengan rumus:
Un = a + (n-1) b
Keterangan :
Un = suku ke n dengan n = 1,2,3, …
a = suku pertama → U1 = a
b = selisih/beda
(1) 3, 7, 11, 15, 19, …
(2) 30, 25, 20, 15, 10,…
Bentuk Barisan Aritmatika
Keterangan:
a = U1 = Suku pertama
b = beda
n = banyak suku
Un= Suku ke-n
Contoh Barisan Aritmatika
- Suku pertama dari barisan aritmatika adalah 3 dan bedanya = 4, suku ke-10 dari barisan aritmatika tersebut adalah …
Penyelesaian:
a = 3
b = 4
- Diketahui barisan aritmatika sebagai berikut: 5, 8, 11, …
Tentukan: Nilai suku ke-15 !
Penyelesaian:
Jika barisan aritmatika mempunyai banyak suku (n) gan
Suku Tengah Barisan Aritmatika
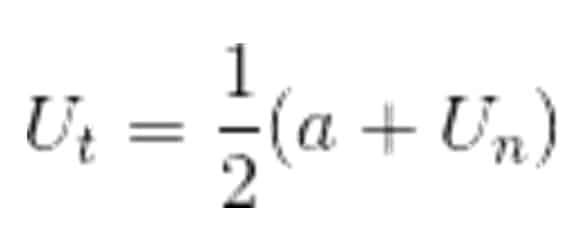
Barisan (l) mempunyai beda, b = 4. Barisan ini disebut barisan aritmetika naik karena nilai suku-sukunya makin besar.
Barisan (2) mempunyai beda, b = -5. Barisan ini disebut barisan aritmetika turun karena nilai suku-sukunya makin kecil.
Suatu barisan U1, U2, U3,….disebut barisan aritmetika jika selisih dua suku yang berurutan adalah tetap. Nilai Untuk menentukan suku ke-n dari barisan aritmetika. perhatikan kembali contoh barisan
U1 = 3 =+ 4 (0)
U2 = 7 = 3 + 4 = 3 + 4 (1)
U3 = 11 = 3 + 4 + 4 = 3 + 4 (2)
….
Un = 3 + 4(n-1)
Secara umum, jika suku pertama (U1) = a dan beda suku yang berurutan adalah b maka dari rumus Un = 3 + 4(n – 1) diperoleh 3 adalah a dan 4 adalah b. Oleh sebab itu, suku ke-n dapat dirumuskan
Un = a + b(n-1)
Barisan aritmetika yang mempunyai beda positif disebut barisan aritmetika naik, sedangkan jika bedanya negatif disebut barisan aritmetika turun.
U1, U2, U3, …….Un-1, Un disebut barisan aritmatika, jika
U2 – U1 = U3 – U2 = …. = Un – Un-1 = konstanta
Un = a + (n-1)b = bn + (a-b) → Fungsi linier dalam n
Contoh Barisan Aritmatika :
Tentukanlah suku ke 15 barisan 2, 6, 10, 14, …
Jawab:
n = 15
b = 6-2 = 10 – 6 = 4
U1 = a = 2Un = a + (n-1) b
U15 = 2 + (15-1)4
= 2 + 14.4
= 2 + 56 = 58
Diketahui barisan aritmetika 3, 8, 13, …
- Tentukan suku ke-10 dan rumus suku ke-n barisan tersebut!
- Suku keberapakah yang nilainya 198 ?
Jawab :
- Dari barisan aritmetika 3, 8, 13, … diperoleh suku pertama a = 3 dan beda b = 8 – 3 = 5.
Un = a + (n – 1)b
U10 = 3 + (10 – 1)5
= 3 + 9 x 5
= 3 + 45
= 48
Un = a + (n – 1)b
= 3 + (n – 1)5
= 3 + 5n – 5
= 5n – 2
- Misalkan Un = 198, maka berlaku :
Un = 198
5n – 2 = 198
5n = 200
n = 40
Jadi 198 adalah suku ke- 40
Pengertian Deret Aritmetika (Deret Hitung)
Coba kamu perhatikan barisan aritmetika berikut.
- 3, 6, 9, 12, 15, 18, … , Un
Jika kamu jumlahkan barisan tersebut, terbentuklah deret aritmetika sebagai berikut.
- 3 + 6 + 9 + 12 + 15 + 18 + … + Un
Jadi, deret aritmetika adalah jumlah suku-suku barisan dari barisan aritmetika.
Contoh Soal Deret Aritmatika I
Suatu barisan aritmetika memiliki suku pertama 5 dan beda 3. Tuliskan deret aritmetika dari barisan tersebut.
Jawab:
- Barisan aritmetikanya adalah 5, 8, 11, 14, 17, 20, 23, …, Un
- Deret aritmetikanya adalah 5 + 8 + 11 + 14 + 17 + 20 + 23 + … + Un
Rumus Deret Aritmatika
Sekarang, bagaimana cara menjumlahkan deret aritmetika tersebut? Untuk deret aritmetika yang memiliki suku-suku deret yang sedikit mungkin masih mudah untuk menghitungnya.
Sebaliknya, jika suku-suku deret tersebut sangat banyak, tentu kamu akan memerlukan waktu yang cukup lama untuk menghitungnya.
Berikut ini akan diuraikan cara menentukan jumlah n suku pertama deret aritmetika. Misalkan, Sn adalah jumlah n suku pertama suatu deret aritmetika maka;
Jadi, rumus untuk menghitung jumlah suku-suku deret aritmetika adalah sebagai berikut.
Oleh karena Un = a + (n – 1) b, rumus tersebut juga dapat ditulis sebagai berikut.
Contoh Soal Deret Aritmatika II
Diketahui deret aritmetika : 3 + 7 + 11 + 15 + 19 + … + U10. Tentukan:
a. suku kesepuluh (U10) deret tersebut,
b. jumlah sepuluh suku pertama (S10).
Diketahui suatu deret aritmetika dengan suku pertama 10 dan suku keenam 20.
a. Tentukan beda deret aritmetika tersebut.
b. Tuliskan deret aritmetika tersebut.
c. Tentukan jumlah enam suku pertama deret aritmetika tersebut.
Sifat-sifat Deret Aritmatika
Sekarang, kamu akan mempelajari sifat-sifat deret arimetika. Suatu deret aritmetika memiliki sifat-sifat sebagai berikut.
Untuk lebih jelasnya, perhatikan contoh-contoh soal berikut.
Contoh Soal Deret Aritmatika III
2. Dari suatu deret aritmetika diketahui bahwa suku keempatnya adalah 38 dan suku kesepuluhnya adalah 92. Tentukan:
a. beda deret aritmatika tersebut,
b. suku ketujuh deret aritmetika tersebut.
- Get link
- X
- Other Apps
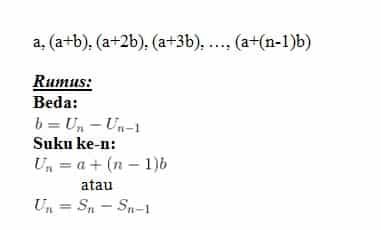
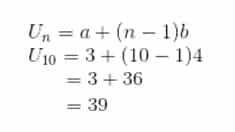

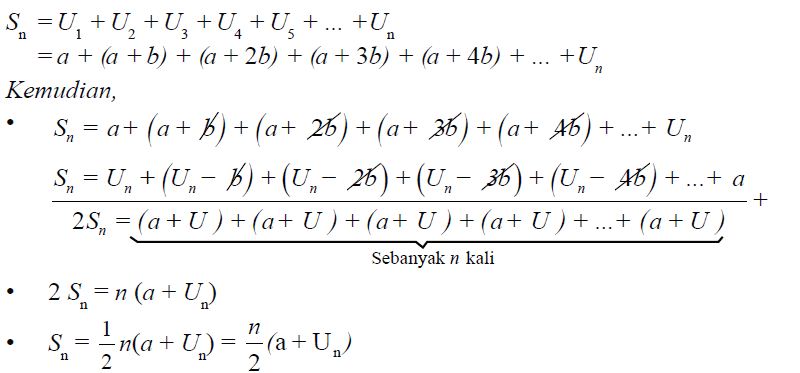
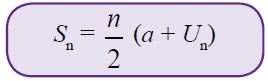








Comments
Post a Comment